Função seno
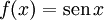
Associa a cada número real x o número y = senx
Amplitude: 1 que por sua vez é o mesmo valor do raio do círculo trigonométrico onde ela foi definida.
Domínio: Como x pode assumir qualquer valor real: D = R
Período: É sempre o comprimento da senóide. No caso da função 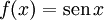 , a senóide caracteríza-se pelo intervalo de 0 a 2π, portanto o período é 2π.
, a senóide caracteríza-se pelo intervalo de 0 a 2π, portanto o período é 2π.
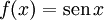 , a senóide caracteríza-se pelo intervalo de 0 a 2π, portanto o período é 2π.
, a senóide caracteríza-se pelo intervalo de 0 a 2π, portanto o período é 2π.Conjunto Imagem: Como seno possui valor máximo e mínimo, que são respectivamente 1 e -1, o conjunto imagem se encontra no intervalo entre esses valores: ![\operatorname{Im} = [-1, 1]](http://upload.wikimedia.org/math/8/9/e/89efdaea105b3963eb51d030df18585f.png)
![\operatorname{Im} = [-1, 1]](http://upload.wikimedia.org/math/8/9/e/89efdaea105b3963eb51d030df18585f.png)
Gráfico: Ele sempre se repete no intervalo de 0 a 2π. Esse intervalo é denominado senóide. Para construir o gráfico basta escrever os pontos em que a função é nula, máxima e mínima no eixo cartesiano.
Função cosseno

Associa a cada número real x o número y = cosx
Amplitude: 1
Domínio: Como x pode assumir qualquer valor real: D = R
Período: É sempre o comprimento da cossenóide. No caso da função f(x) = cos x , a cosenóide caracteriza-se pelo intervalo de 0 a 2π, portanto o período é 2π.
Conjunto Imagem: Como cosseno possui valor máximo e mínimo, que são respectivamente 1 e -1, o conjunto imagem se encontra no intervalo entre esses valores: ![\operatorname{Im} = [-1, 1]](http://upload.wikimedia.org/math/8/9/e/89efdaea105b3963eb51d030df18585f.png)
![\operatorname{Im} = [-1, 1]](http://upload.wikimedia.org/math/8/9/e/89efdaea105b3963eb51d030df18585f.png)
Gráfico: Ele sempre se repete no intervalo de 0 a 2π. Esse intervalo é denominado cossenóide. Para construir o gráfico basta escrever os pontos em que a função é nula, máxima e mínima no eixo cartesiano.
Função tangente

Associa a cada número real x o número y = tgx
Domínio: A função da tangente apresenta uma peculiaridade. Ela não existe quando o valor decosx = 0 (não existe divisão por zero), portanto o domínio são todos os números reais, exceto os que zeram o coseno.
Período: π
Conjunto Imagem: ![\operatorname{Im} = \left]-\infty, \infty \right[](http://upload.wikimedia.org/math/a/4/0/a40542781d0533e14250e9dca474615b.png)
![\operatorname{Im} = \left]-\infty, \infty \right[](http://upload.wikimedia.org/math/a/4/0/a40542781d0533e14250e9dca474615b.png)
Gráfico: Tangentóide.
Fonte: http://migre.me/5y0TC
quase o que eu queria.mas ta bom
ResponderExcluir100%
ResponderExcluirmuito bom (y)
ResponderExcluirmuito bom vei bem resumido
ResponderExcluirAjudou um pouco.
ResponderExcluirajudou muito !
ResponderExcluirmas, eu queria uns exemplos sobre imagem..
eu precisava de mais 1 exemplo de cada....
ResponderExcluirEste é um excelente conteúdo,mas para que quer mais aprofundar práticamnte sugiro este canal onde você vai aprender a matemática de forma muito didática e simples, isto lhe garanto você não vai se arrepender, inscreva-se no canal Kutaya Explica-me:
Excluirhttps://www.youtube.com/watch?v=SmEX1bkB9ig
Ufa, clareou! Difícil encontrar algo objetivo quando o assunto é este.
ResponderExcluirMuito grato!
Maicon
O melhor resumo que achei sobre o assunto.
ResponderExcluirGratidão!
n me ajudou em nada muito explicado
ResponderExcluirgostei
ResponderExcluirperfeitoo !!
ResponderExcluirme ajudou bastante, muito bom :)
ResponderExcluirMuito bom o resumo, me ajudou bastante!!! Grato.
ResponderExcluirMe ajudou muito
ResponderExcluirMe ajudou. Bem reduzido e claro
ResponderExcluirMe ajudou. Bem reduzido e claro
ResponderExcluirCara muito obg msm , vc ajudou muito na pesquisa do meu trabalho , obg
ResponderExcluirEste é um excelente conteúdo,mas para que quer mais aprofundar práticamnte sugiro este canal onde você vai aprender a matemática de forma muito didática e simples, isto lhe garanto você não vai se arrepender, inscreva-se no canal Kutaya Explica-me:
ResponderExcluirhttps://www.youtube.com/watch?v=SmEX1bkB9ig
Excelente!
ResponderExcluirfalta cotg n gostei
ResponderExcluirEste comentário foi removido pelo autor.
ResponderExcluirbrigado!!
ResponderExcluirme ajudou muitoooo!!
:D
Gostei, bastante resumido, mais esta bom!
ResponderExcluirfaltou explicar um pouquinho mais a tangente, ja que a maioria dos alunos tem mais problemas com essa função!
Muito grato!
Maravilhoso! Simples e direto. Era exatamente o que eu precisa.
ResponderExcluirmuito bom mesmo , gostei ...obg
ResponderExcluir